一種縫合 Gradient Noise 的技巧

A Technique to Quilting Gradient Noise

目的

我想在一個 torus 的空間中使用演算法生成地形 (Procedural generation)，因此演算法必須使地圖邊界無接縫 (Seamless)。

被排除的方案

The image quilting

該算法的原理是在兩張貼圖的交界處做重疊 (overlay)，並使用 error 值尋找最短路徑而達到縫合的目的。^{1 2}

但是該算法的目的是從原始貼圖中抽出拼貼塊 (patches)，並用拼貼塊重新製作圖片，並不適合用於兩個固定邊界的縫合。

當我試著用這個算法處理 noise map 的交界會變成這樣：

Periodic Perlin Noise

Perlin Noise 的產生是透過在網格中指定隨機的向量來創造梯度，再透過內插來生成最終的 noise map。

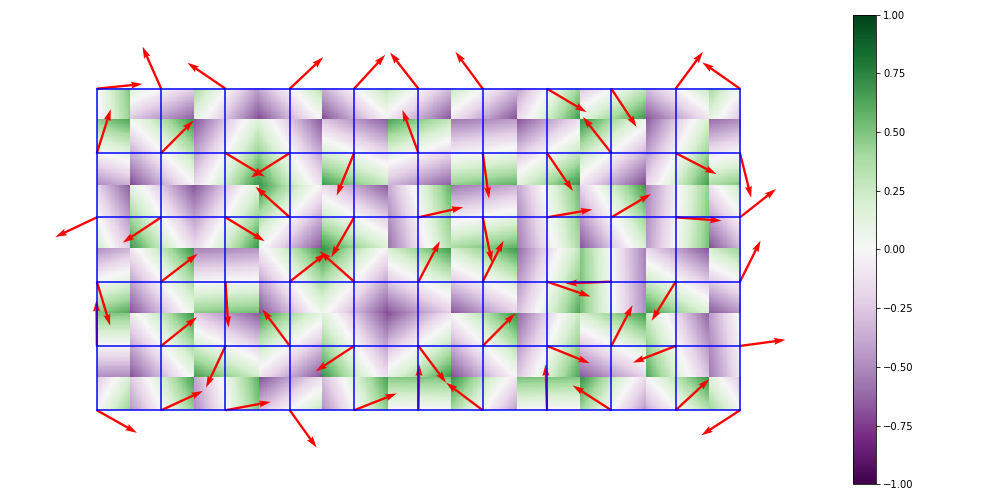
因此只要兩個邊界使用同一組向量，就能生成無接縫的 noise map。³

不過我個人不太想重新實做 noise 生成層級的演算法；加上雖然我的目標是生成無接縫的 noise map，但是很有可能實際上會需要縫合兩張算法完全不同的 noise map，再加上交界處很有可能不具有完整的網格（貼圖的大小不是 lattice 的整數倍），所以最終不考慮這個方案。

演算法

其實就是做線性內插：

$$f(x) = \begin{cases} g(x), & x < x_a \\ v(x), & x_a \leq x \leq x_b \\ h(x), & x_b < x \end{cases} \\ v(x)=g(x) \cdot (1-r) + h(x) \cdot r \\ r(x)=\frac{x-x_a}{x_b-x_a}$$

只是線性內插本質上就是加權平均數，這會使 noise map 變得模糊，因此加上一個修飾：

$$v_s(x) = \text{smoothstep}(v) \cdot r_s + v(x) \cdot (1-r_s ) \\ r_s(x) = \begin{cases} r, & r \leq 0.5 \\ (1-r), & r > 0.5 \end{cases}$$

smoothstep 函數能夠增加 noise 的對比來修復部份因為線性插值造成銳利度降低（模糊）的區域。

沒有 smoothstep：

加上 smoothstep：

Footnotes

1. Image Quilting for Texture Synthesis and Transfer. (Alexei A. Efros). Retrieved 2022-06-04, from https://people.eecs.berkeley.edu/~efros/research/quilting/quilting.pdf ↩

2. Image Quilting for Texture Synthesis & Transfer. (Alexei Efros). Retrieved 2022-06-04, from https://people.eecs.berkeley.edu/~efros/research/quilting/efros-siggraph01.ppt ↩

3. tiles - How do you generate tileable Perlin noise? (Boojum). Retrieved 2022-06-04, from https://gamedev.stackexchange.com/questions/23625 ↩