Skip to main content

熵庫 (Entropy Reservoir) 假說

· 10 min read
Wei Ji

熵—衡量萬物混亂程度的物理量...嗎？​

熵 (Entropy) 具有很多種表述方式，比如：

  • 克勞修斯熵 dS=δqTd S = \frac{\delta q}{T}
  • 波滋曼熵 S=kln⁡WS = k \ln W
  • 資訊熵（夏農熵） S=log⁡22N=NS = \log_2 2^N = N

有一種熵的詮釋與「狀態所包含的排列數」相關，波滋曼熵與夏農熵便是如此。以波滋曼熵為例，當中的 W 所代表的意義是微觀物理的狀態數1：

W=N!∏iNi!W={\frac {N!}{\prod _{i}N_{i}!}}

夏農熵中 2N2^N 則是在 N bit 的空間中；資訊有幾種排列方式。夏農熵有另外一種表述方式2，在此就先不贅述。

總之先擲點硬幣吧！​

現在想像一個盒子內裝有 n 枚硬幣，當我隨意上下搖晃盒子，內部的硬幣就會以一半反面一半正面的機率翻面。

我們可以發現 k 枚硬幣正面朝上的排列數可以寫作：

W=n!k!(n−k)!W = \frac{n!}{k!(n-k)!}

以 n=10 為例，我們對 W(k) 作圖：

我們可以發現當 k=n2k=\frac{n}{2} 的時候排列數最多，若依照熵的定義；此時的熵應該也是最大的。

熵的相對性​

雖然特定狀態的排列數可以定義出該狀態的熵值，但是實務上我們考慮的是「熵的變化」：

ΔS=S1−S0\Delta S = S_1 - S_0

畢竟當系統十分龐大時，你很難計算或窮舉出它的所有可能的排列（數）。

機率使其往高熵發展​

根據經驗，我們知道隨著搖晃盒子，硬幣正面、反面朝上的分佈應該會是一半一半。但是我們如何用數學解釋這個現象呢？

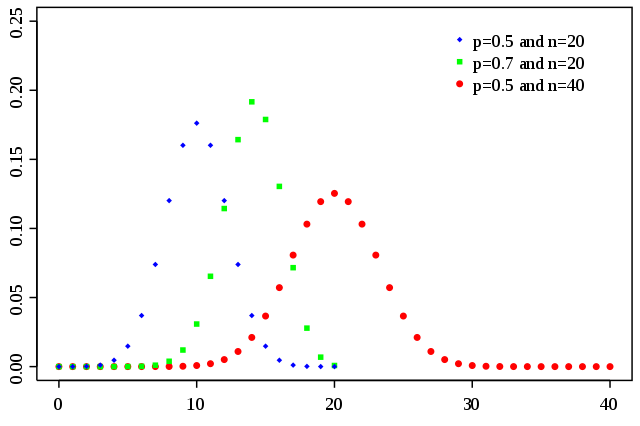
這個將硬幣放在盒子內的實驗，可以視作伯努力試驗，而伯努力試驗又可以用二項式分佈來描述：

f(k,n,p)=Pr⁡(X=k)=n!k!(n−k)!pk(1−p)n−k f(k,n,p)=\Pr(X=k)=\frac{n!}{k!(n-k)!}p^{k}(1-p)^{n-k}

kk：成功的次數，在本例的情況是指正面朝上的硬幣數目 nn：進行試驗的次數，在本例的情況是指總共有多少枚硬幣 pp：成功的機率，在本例就是正面朝上的機率，也就是 0.5 Pr⁡\Pr：機率密度

3

二項式分佈若繪圖會得到上述圖形，y 軸是機率密度，x 軸則是 k 值。可以看到它的分佈趨近常態分佈。根據二項式分佈的特性我們可以得到其標準差為：

σ=np(1−p).\sigma = \sqrt{np(1-p)}.

隨著 n 增大，其標準差佔整體的比例會越來越窄4：

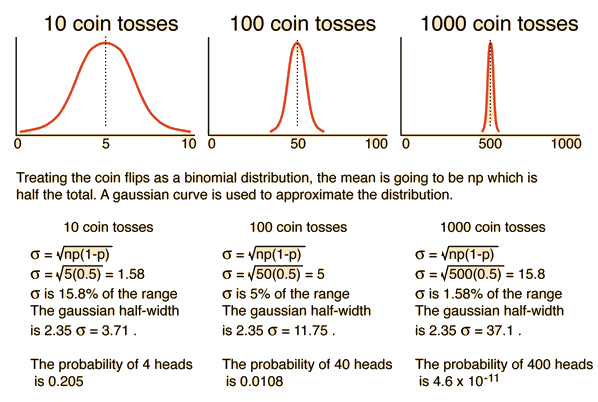
若考慮 1,000 枚硬幣，標準差為 15.8 ，跨越 3 個標準差的距離為 453 ~ 547，這代表有 99.7% 的機率，正面朝上的硬幣數量會在 453 ~ 547 這個區間內。

若考慮 1,000,000 枚硬幣，標準差為 500 ，跨越 3 個標準差的距離為 498,500 ~ 501,500，這代表有 99.7% 的機率，正面朝上的硬幣數量會在 498,500 ~ 501,500 這個區間內。

我們可以發現當 n 增大，機率分佈會聚集在少數的某些狀態，而其他狀態發生的機率便顯得微乎其微。

有人說熵就是亂度？​

我們可以注意到機率分佈會集中在 k=n2k=\frac{n}{2} 附近，而 k=n2k=\frac{n}{2} 時又是熵最大的狀態，因此我們可以注意到熵越大的狀態越容易自然發生。

不管我怎麼排列這些硬幣，只要隨著搖晃盒子，硬幣的分佈都會往熵最大的狀態發展。令我排列的狀態熵為 S0S_0 ，而最終狀態的熵為 S1S_1 則：

Δ S>0\Delta\,S>0

不論你從何種狀態往最終狀態變化，其 Δ S\Delta\,S 必定大於 0。這就是熱力學第二定律。

當我們排列硬幣時，會下意識的將該狀態視為「有序」，而經過搖晃盒子後，硬幣的分佈狀態則下意識地視作「混亂」，因此看似萬物都會自然往混亂發展，如此以來熵似乎就和混亂掛勾了，似乎熵能夠描述事物的「混亂程度」。「秩序」與「混亂」的狀態其實是相當抽象且無法被明確定義的，「熵代表著混亂的程度」是一種通俗的理解方式，但是也是相對不嚴謹的理解方式。

資訊的不確定性與熵的關係​

我們來看看兩組資料，其中 x 代表可以為 1 也可以為 0 ，是一個不確定的資料：

  1. 10101010
  2. 10x01x10

根據熵與排列數之間的關係，我們可以發現第一組資料的排列數只有 1 種，後者的排列數則有 4 種，也就是後者的熵較高。

資訊體生物的空想實驗​

首先想像一個資訊生物，其所承載的資訊會影響這個生物的各種性狀 (Phenotypic trait)，它的資訊是完全明確的，並且任一位元的資訊發生變化就會造成系統異常（遺傳疾病）從而造成生物整體的崩潰：死亡。

接著想像另外一個資訊生物，他有部份的資訊是不確定的，也就是資訊為 1 還是 0 所表現出的性狀皆不會對本體造成關鍵的危害。

想像這兩隻資訊生物被放置於同一個環境之中，前者因為不容許任何錯誤，其後代資訊一定是完全複製的，因為複製錯誤的都會死亡；另外一隻的後代則容許一定程度的變化，這個變化也包含資訊數變多。

不難想像在長時間的迭代中，後者遲早會發展出更多的競爭競爭優勢。如果兩種生物處於相同的環境之中，不會（無法）發生變化的資訊生物會漸漸的在競爭中消失。

熵庫 (Entropy Reservoir) 與熵池 (Entropy pool)​

資訊生物的資訊都能夠被描述成不確定的部份以及確定的部份，如：

I=(1011010XX0100011XX010101100XXX)=(XXXXXXX)(1011010,0100011,010101100,)\begin{aligned} I = (1011010XX0100011XX010101100XXX) \\ = (XXXXXXX)(1011010,0100011,010101100,) \end{aligned}

並且任意資訊都能被母體集合 PP 包含：

∀I,I⊂P\forall I, I \subset P

這個 PP 就是熵庫 (Entropy Reservoir)，理想熵庫是一個無限大的集合，而且充滿了不確定的資訊。被資訊生物收錄的不確定資訊則稱為熵池 (Entory Pool)，任何能夠描述具有競爭優勢的性狀的資訊皆來自不確定資訊的收斂。

描述競爭優勢的確定資訊必須由熵池中的不確定資訊收斂而來；不確定資訊則必須從熵庫獲得。 我們可以將獲得資訊的過程想像成一種開採資源的過程，這種資源必須從不確定資訊收斂而來，而不確定資訊又必須從熵庫中開採，並且整個過程消耗著時間與能源。

創用 CC 授權條款
Wei Ji以創用CC 姓名標示-相同方式分享 4.0 國際 授權條款釋出。

Footnotes​

  1. Boltzmann's entropy formula - Wikipedia. (n.d.). Retrieved 2019-11-17, from https://en.wikipedia.org/wiki/Boltzmann%27s_entropy_formula ↩

  2. Entropy (information theory) - Wikipedia. (n.d.). Retrieved 2019-11-17, from https://en.wikipedia.org/wiki/Entropy_(information_theory) ↩

  3. Binomial distribution - Wikipedia. (n.d.). Retrieved 2019-11-17, from https://en.wikipedia.org/wiki/Binomial_distribution ↩

  4. Comments on Statistical Methods. (n.d.). Retrieved 2019-11-17, from http://hyperphysics.phy-astr.gsu.edu/hbase/Kinetic/statcom.html ↩