工程數學筆記 - 通俗的理解卷積運算 (convolution)

前言（a.k.a. 廢話）

我修過不少次工程數學，每次都選不同老師的課，因此目前修課老師在個人經驗中算是教學相對熱忱、詳細的；在課程中安插講解實務上的應用場合，用彈簧-質點-阻尼模型來解釋這些解微分方程的方法如何處理實際的物理問題。

最近課程進度到達拉普拉斯章節中的卷積性質，很驚訝他沒有花太多時間在解釋卷積，而是直接依照數學定義開始計算，並且示範其性質，於是我就這樣盯著那個積分方程式整整一節課，想著這玩意兒的幾何意義。(˘•ω•˘)

定義

下課之後我去查詢卷積的定義：

$$\int _{-\infty }^{\infty }f(\tau )g(x-\tau )\,\mathrm {d} \tau$$

恩？這東西的上下限怎麼跟我在課堂上看到的不一樣？接著我找到了一段話[^zero]：

For functions f, g supported on only [0, ∞) (i.e., zero for negative arguments), the integration limits can be truncated

在工程上函數可以代表訊號，而實務上我們不會考慮時間小於 0 的訊號，並且我們通常也只需要關注一小段時間內的行為，從而產生一個卷積特例：

$$\int _{0}^{t}f(\tau )g(t-\tau )\,\mathrm {d} \tau$$

讓我們先專注於這個特例，廣義的卷積等等再回來看。

幾何解釋

本文的重點其實就是一張圖：

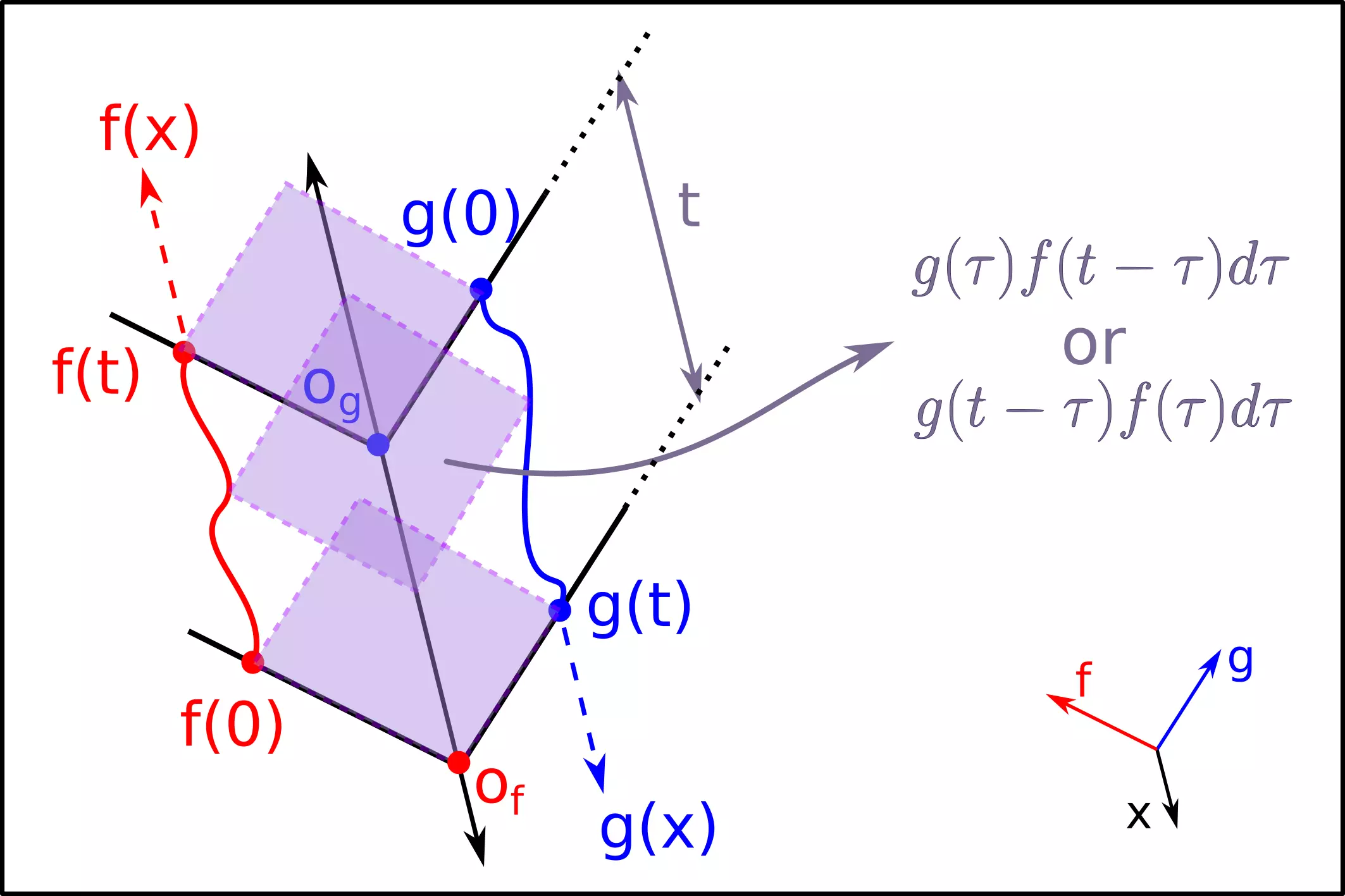
在一個三維空間中，f 和 g 分別在兩個互相垂直的平面上，並且方向相反， 看起來就像是兩個函數彼此擦肩而過。

可以看出 $g(\tau)f(t-\tau)$ 或是 $g(t-\tau)f(\tau)$ 便是兩函數相乘後得到的長方形面積， 乘上上 $d \tau$ 的話就會變成「一片微量的體積」了， $g(\tau)f(t-\tau) d \tau$ 與 $g(t-\tau)f(\tau) d \tau$ 的差異來自於： 你是站在 $f(x)$ 的系統上積分還是站在 $g(x)$ 的系統上積分。

積分過後你會得到一條像是烤土司的東西，而這條土司的體積可以描述為：

$$\begin{align} V &= \int_0^t A(\tau)d\tau \\ &= \int_0^t g(\tau)f(t-\tau) d \tau \\ &= \int_0^t g(t-\tau)f(\tau) d \tau \end{align}$$

這個體積就是我們的卷積了。

廣義卷積的幾何解釋

即使上下限變成無限，總之還是可以用烤土司得方式去思考， 我們不難發現如果兩個函數不會收斂的話，卷積是沒有意義的，因為這會是一條體積無限大的土司（？）

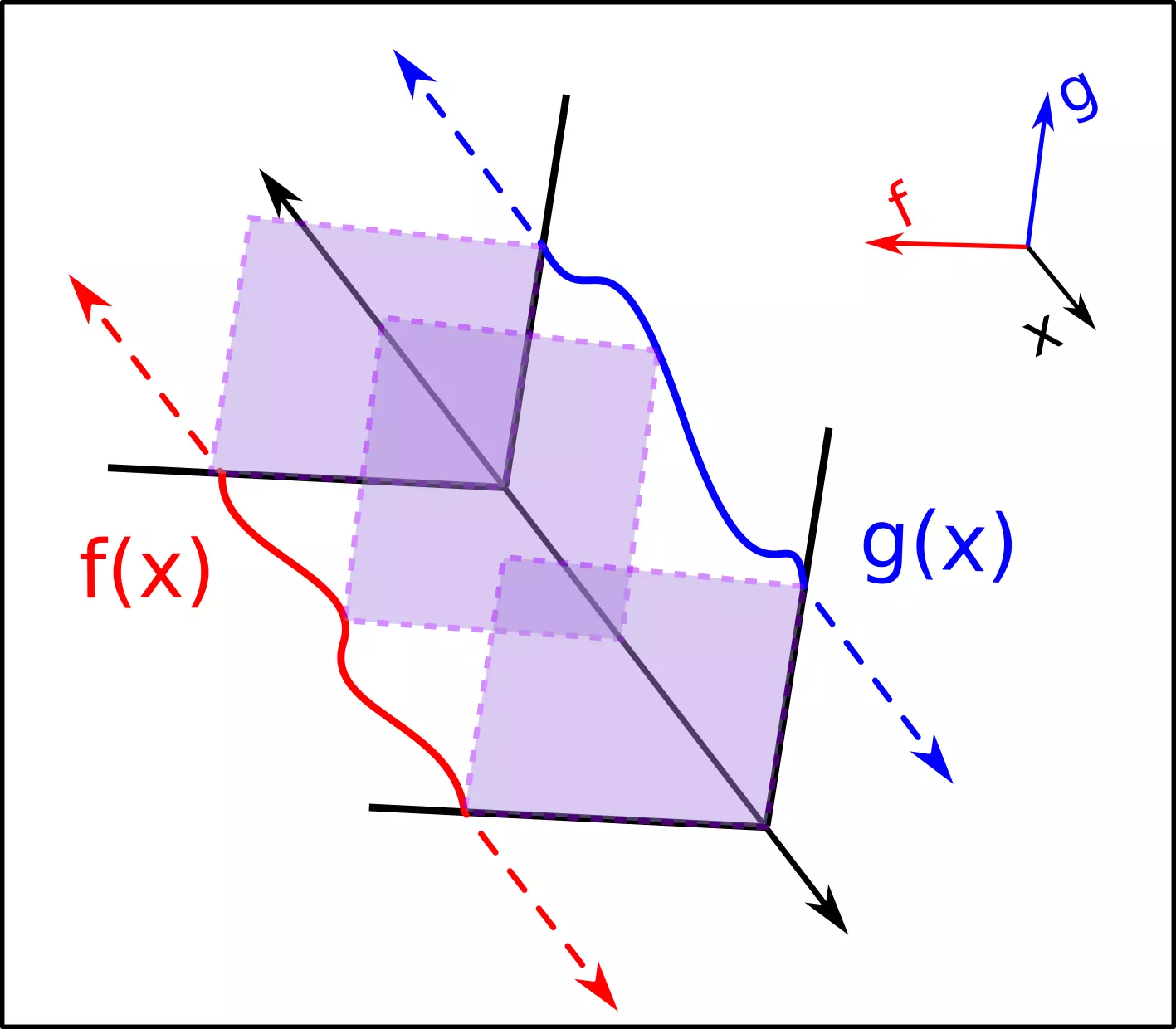
※或許在數學上有其他用途或意義，不過以工程而言沒什麼作用，不難理解為什麼在工程數學裡函數被約束成有限的時間區間。

值得注意的是，如果 $f(x)$ 和 $g(x)$ 在 $x$ 小於零的時候，其值都為零， 依照卷積的定義會很自然的把兩端以外的函數乘以零，只留下一條長度為 $t$ 的土司：

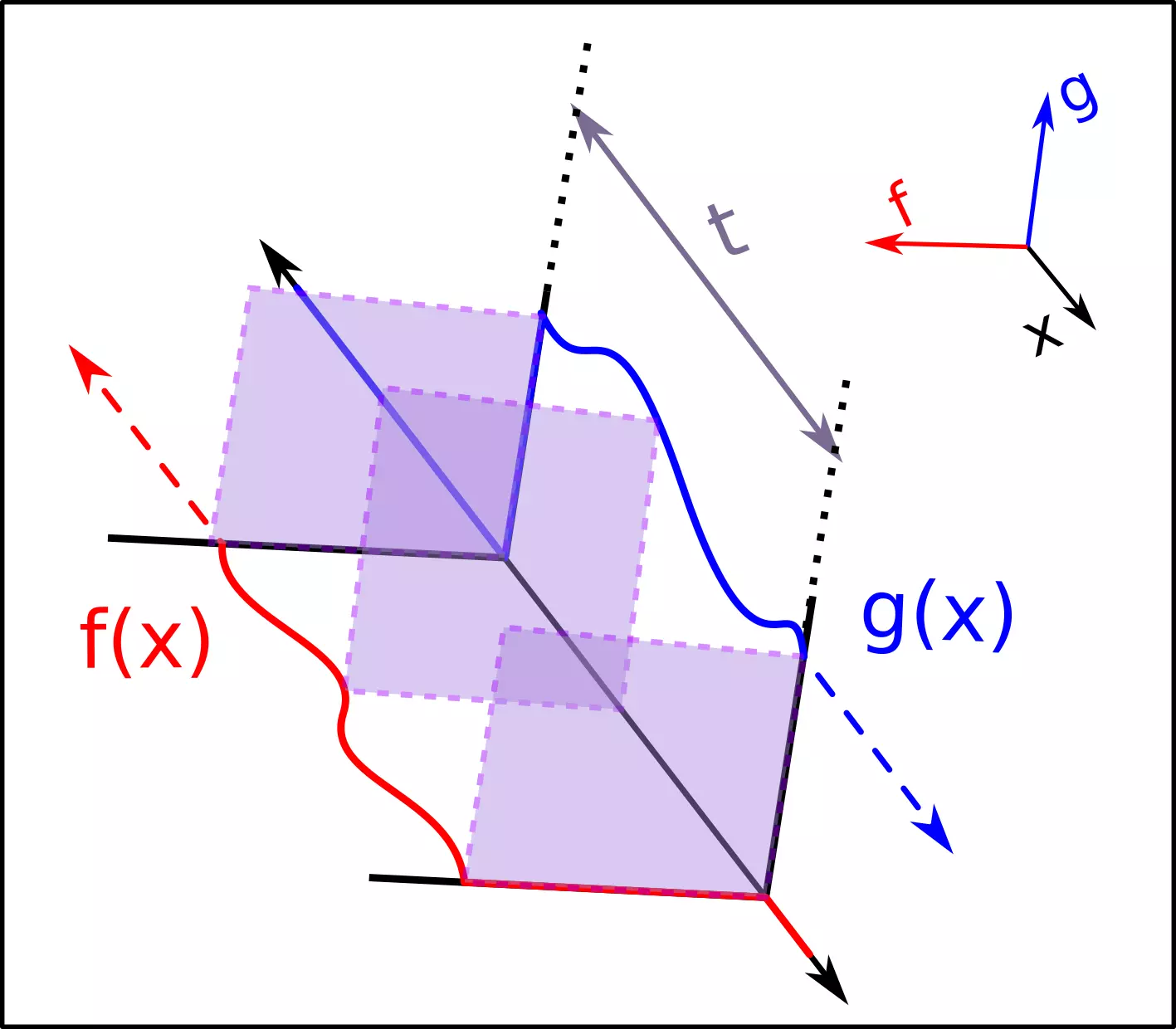
這條截斷的土司就是工程上使用的卷積積分方程。

物理意義

幾何意義看起來是條烤土司，不過究竟什麼樣的物理環境會用到這個數學模型呢？🤔

我在網路上找到了一個關於饅頭的例子[^example]：

有一個饅頭工廠，能夠生產饅頭，同時，饅頭放久了會壞掉， 我們可以用一些符號描述這件事：

• $f(t)$：工廠生產饅頭速率與時間的關係（單位：個饅頭/單位時間）
• $g(t)$：饅頭的生存函數，描述尚未壞掉的饅頭比率與時間的關係（單位：好饅頭/總饅頭）

接著我們提出一個問題：

n 個單位時間之後，我們有多少沒壞的饅頭？

如果我們先用離散方式描述，在第 0 個單位時間生產的饅頭會放 n 個單位時間， 因此在 n 個單位時間後殘留的饅頭數量可以表示成： $f(0)g(n)$ ， 在第 1 個時間單位生產的饅頭會放上 n-1 個時間單位，寫作：$f(1)g(n-1)$， 我們可以歸納出： $f(x)g(n-x)$， 最後把所有瞬間的情況積分起來就會得到：

$$\int_0^n f(x)g(n-x) dx$$

卷積的積分方程就這樣出現在我們眼前了！(⊙ω⊙)

---

Wei Ji以創用CC 姓名標示-相同方式分享 4.0 國際 授權條款釋出。